ホーム
Pythonでデータ分析
Pythonでデータ分析入門1（初めての回帰分析）

Pythonでデータ分析入門1（初めての回帰分析）

Pythonを使って重回帰分析をしてみます。

本投稿のコードは、Jupyter Notebook上で実行しています。コンソールで実行する場合は、適宜plotなどの表示用命令を追加してください。

回帰分析とは
分析するデータ
データの読み込みとデータそのものの確認
データ間の関係を確認する
元データを学習用と検証用に分割する
モデルの学習と性能評価をする
モデルを改善する

回帰分析とは

独立変数（説明変数）Xと従属変数（目的変数）Yの関係を推計することを、回帰分析（regression analysis）と言います。

下記の数式のようなモデルに当てはめてパラメータ（aとb）を求める場合を線形回帰と言います。非線形のモデルもあります。

Xが1次元の場合は単回帰、2次元以上の場合は重回帰と言います。

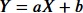
今回は、線形の重回帰分析を行います。

分析するデータ

seabornに備わっているdiamondsというサンプルデータで試してみます。

daiamondsデータセットは、ダイアモンドの価格と石のサイズや色味などの情報をcsv形式にまとめたデータセットです。

列名	内容
carat	重さ
cut	形
color	色
clarity	透明度
depth	高さ
table	表面の大きさ
price	価格
x	寸法
y	寸法
z	寸法

caratなどの石の情報から、重回帰分析を使ってpriceを推定します。

データの読み込みとデータそのものの確認

必要なモジュールをインポートして、データを読み込みます。

>>> import pandas as pd
>>> import seaborn as sns
>>> import numpy as np
>>> data = sns.load_dataset('diamonds')

seabornのデータセットの読み込みについては、「pandasの学習用データセットを入手する」を参照してください。

データに欠損値がないか、確認をします。

>>> data.isnull().sum()
carat      0
cut        0
color      0
clarity    0
depth      0
table      0
price      0
x          0
y          0
z          0
dtype: int64

このデータセットには欠損値はありませんでした。

欠損値が存在する場合は、欠損値を含むデータを削除したり、欠損値を何か他の値で置き換えるなどの前処理を行います。

欠損値の扱いについては、「Pythonでpandas入門5（欠損値（NaN）の扱い）」を参照してください。

データ間の関係を確認する

数値データ

数値データの分布を見てみます。

>>> data.describe()

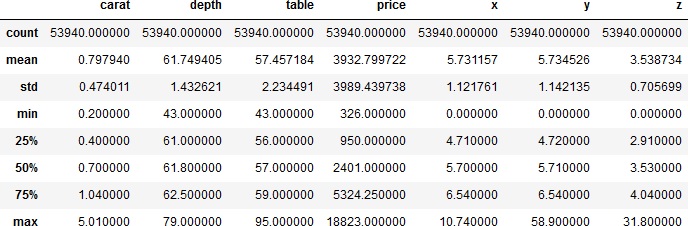
各数値データ間の関係を可視化してみます。

>>> sns.pairplot(data)

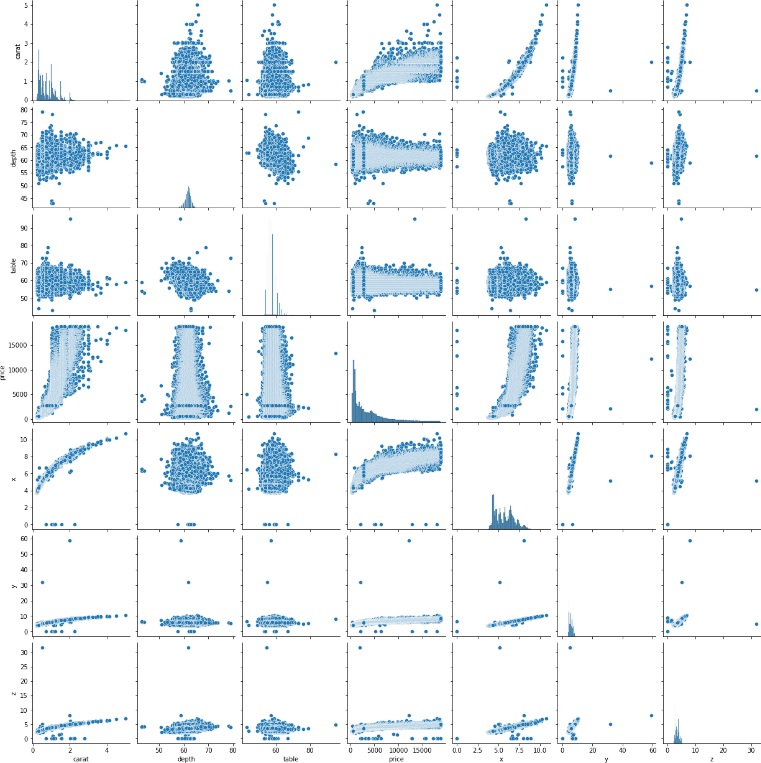
各数値データ間の相関係数を求めてみます。

>>> data.corr()

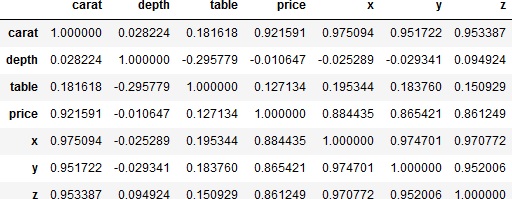
price（価格）とcarat（重さ）が、ばらつきはあるものの比例っぽい関係にあるようです。

caratとx、y、zはかなり1対1に近い関係にある感じです。まあ、どの石も比重はあまりかわらないでしょうから、重さと体積は概ね比例するのでしょう。

カテゴリデータ

カテゴリデータの分布を見てみます。数値ではなく、文字列などで分類されたデータです。

>>> sns.boxplot(x='cut', y='price', data=data)
>>> sns.boxplot(x='color', y='price', data=data)
>>> sns.boxplot(x='clarity', y='price', data=data)

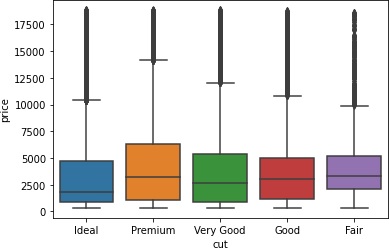
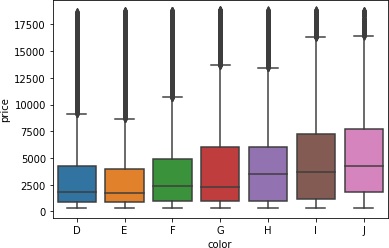
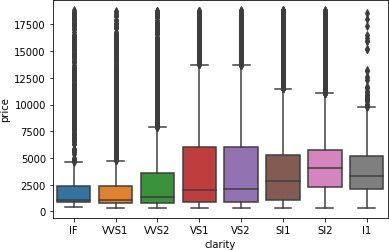
clarity（透明度）など相関ありそうですけど、よくわからないですね。普通に考えれば、透明なほど高価なイメージがありますが。

clarityのデータの偏りを見てみます。

>>> data['clarity'].value_counts(sort=False)
IF       1790
VVS1     3655
VVS2     5066
VS1      8171
VS2     12258
SI1     13065
SI2      9194
I1        741
Name: clarity, dtype: int64

頻度にだいぶばらつきがありますね。IFが最も透明度が高いので高価になりやすいはずですが、母数に対してばらつきが大きいのかもしれません。

元データを学習用と検証用に分割する

これからモデルの学習を行うわけですが、モデルの学習が終わったら、学習したモデルがどの程度の性能を持つのかを確認しなければなりません。

そこで元のデータを、学習用のデータとモデルの性能の検証用のデータに分割します。

>>> from sklearn.model_selection import train_test_split
>>> train, test = train_test_split(data, test_size=0.3, random_state=0)

ここでは、学習用データを元データの70%、テスト用のデータを30%に分割しました。詳しくは「Pythonでデータを学習用と検証用に分割する」を参照してください。

モデルの学習と性能評価をする

必要なモジュールをインポートします。

Scikit-learnの線形回帰モデル（LinearRegression）を使用します。性能評価には、RMSE（二乗平均平方根誤差）を使用します。

>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.metrics import mean_squared_error

学習用データと検証用データから、説明変数と目的変数を取り出します。

今回は、説明変数としてcaratのみを、目的変数としてpriceを選択します。

>>> train_X = train[['carat']]
>>> train_y = train['price']
>>> test_X = test[['carat']]
>>> test_y = test['price']

では学習をしてみます。

LinearRegressionのオブジェクトを生成した後、そのオブジェクトのfitメソッドに学習用の説明変数と目的変数を渡してモデルの学習を行います。

学習が終わったら、オブジェクトのpredictメソッドに検証用の説明変数を渡すと、学習済みモデルによる推定値が得られます。

>>> lm = LinearRegression()
>>> lm.fit(train_X, train_y)
>>> pred = lm.predict(test_X)

得られた推定値を使って、モデルの性能を確認します。

mean_squared_error関数に真値（検証用データの目的変数（price））と予測値（pred）を渡すと、MSEまたはRMSEをけいさんしてくれます。詳しくは「Pythonで回帰モデルの評価関数」を参照してください。

また、RMSEの値だけを見ても善し悪しが感覚的にわからないので、真値と予測値の散布図をプロットします。散布図が一直線に近いほど（幅が小さいほど）優秀なモデルです。

>>> rmse = mean_squared_error(test_y, pred, squared=False)
>>> print(rmse)
>>> g = sns.relplot(x=test_y, y=pred, aspect=1)
>>> m = np.max([test_y.max(), pred.max()])
>>> g.set(xlim=(0,m))

1540.4224353362183

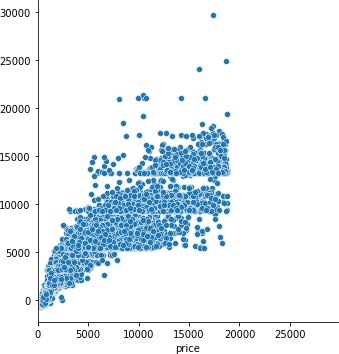
caratだけで推測すると、かなりばらつきがあります。この幅を小さくしたいですね。

モデルを改善する

相関係数の高い数値データを全部説明変数にしてみます。

>>> train_X = train[['carat','x','y','z']]
>>> train_y = train['price']
>>> test_X = test[['carat','x','y','z']]
>>> test_y = test['price']
>>> lm = LinearRegression()
>>> lm.fit(train_X, train_y)
>>> pred = lm.predict(test_X)
>>> rmse = mean_squared_error(test_y, pred, squared=False)
>>> print(rmse)
>>> g = sns.relplot(x=test_y, y=pred, aspect=1)
>>> m = np.max([test_y.max(), pred.max()])
>>> g.set(xlim=(0,m))

1511.5111062851354

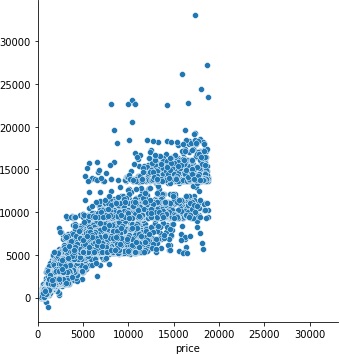
RMSEの数値的には多少良くなりましたが、実用上はあまり効果はありませんでした。そもそもcaratとx、y、zはかなり強い相関がありましたので、caratの特性がモデルに反映されてしまいますからね。

では、カテゴリ変数を数値変数に変換してモデルに学習させてみます。数値データへの変換については、「pandasでカテゴリ変数を数値データに変換する」を参照してください。

データ全体のカテゴリ変数の変換をして、再度学習データと検証データに分割します。

>>> data = pd.get_dummies(data, columns=['cut','color','clarity'])
>>> train, test = train_test_split(data, test_size=0.3, random_state=0)

エンコードしたデータを指定して、学習してみます。

>>> train_X = train[['carat','cut_Ideal','cut_Premium', 'cut_Very Good', 'cut_Good', 'cut_Fair', 'color_D','color_E', 'color_F', 'color_G', 'color_H', 'color_I', 'color_J','clarity_IF', 'clarity_VVS1', 'clarity_VVS2', 'clarity_VS1','clarity_VS2', 'clarity_SI1', 'clarity_SI2', 'clarity_I1']]
>>> train_y = train['price']
>>> test_X = test[['carat','cut_Ideal','cut_Premium', 'cut_Very Good', 'cut_Good', 'cut_Fair', 'color_D','color_E', 'color_F', 'color_G', 'color_H', 'color_I', 'color_J','clarity_IF', 'clarity_VVS1', 'clarity_VVS2', 'clarity_VS1','clarity_VS2', 'clarity_SI1', 'clarity_SI2', 'clarity_I1']]
>>> test_y = test['price']
>>> lm = LinearRegression()
>>> lm.fit(train_X, train_y)
>>> pred = lm.predict(test_X)
>>> rmse = mean_squared_error(test_y, pred, squared=False)
>>> print(rmse)
>>> g = sns.relplot(x=test_y, y=pred, aspect=1)
>>> m = np.max([test_y.max(), pred.max()])
>>> g.set(xlim=(0,m))

1153.7208491090405

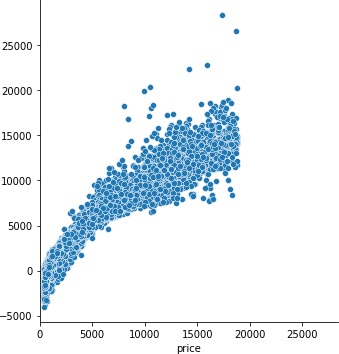
だいぶ良くなりました。

では、突っ込めるデータは全部突っ込んでみましょう。

>>> train_X = train[['carat','depth', 'table','x', 'y', 'z','cut_Ideal','cut_Premium', 'cut_Very Good', 'cut_Good', 'cut_Fair', 'color_D','color_E', 'color_F', 'color_G', 'color_H', 'color_I', 'color_J','clarity_IF', 'clarity_VVS1', 'clarity_VVS2', 'clarity_VS1','clarity_VS2', 'clarity_SI1', 'clarity_SI2', 'clarity_I1']]
>>> train_y = train['price']
>>> test_X = test[['carat','depth', 'table','x', 'y', 'z','cut_Ideal','cut_Premium', 'cut_Very Good', 'cut_Good', 'cut_Fair', 'color_D','color_E', 'color_F', 'color_G', 'color_H', 'color_I', 'color_J','clarity_IF', 'clarity_VVS1', 'clarity_VVS2', 'clarity_VS1','clarity_VS2', 'clarity_SI1', 'clarity_SI2', 'clarity_I1']]
>>> test_y = test['price']
>>> lm = LinearRegression()
>>> lm.fit(train_X, train_y)
>>> pred = lm.predict(test_X)
>>> rmse = mean_squared_error(test_y, pred, squared=False)
>>> print(rmse)
>>> g = sns.relplot(x=test_y, y=pred, aspect=1)
>>> m = np.max([test_y.max(), pred.max()])
>>> g.set(xlim=(0,m))

1122.2313188683815

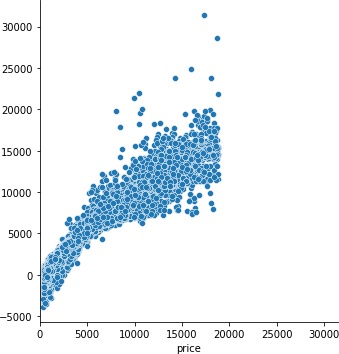
なんでもかんでもデータを突っ込めば良いというわけではないようです。

Pythonで回帰モデルの評価関数 Pythonでデータ分析入門2（初めてのロジスティック回帰（2クラス分類））

公開日 2021-09-12

Pythonでデータ分析入門1（初めての回帰分析）

回帰分析とは

分析するデータ

データの読み込みとデータそのものの確認

データ間の関係を確認する

数値データ

カテゴリデータ

元データを学習用と検証用に分割する

モデルの学習と性能評価をする

モデルを改善する

Pythonでデータ分析カテゴリの投稿

某エンジニアのお仕事以外のメモ（分冊）

Recent Posts

Tags

Categories