Pythonで回帰モデルの評価関数
機械学習(回帰モデル)で利用される評価関数について、Python(Scikit-learn)を使って計算する手順です。
目次
- 残差最大値(MaxError) Maximum residual error
- 平均絶対誤差(MAE) Mean Absolute Error
- 平均二乗誤差(MSE) Mean Squared Error
- 二乗平均平方根誤差(RMSE) Root Mean Squared Error
- 各誤差を計算してみる
残差最大値(MaxError) Maximum residual error
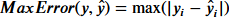
観測値と予測値の差の最大値。
from sklearn.metrics import max_error
ret = max_error(y_true, y_pred)
変数 |
型 |
内容 |
|---|---|---|
y_true |
array-like |
正しい値(観測値) |
y_pred |
array-like |
予測値 |
ret |
float |
差の最大値 |
y_trueとy_predの型は、リストやpandas.Seriesなどです。
戻り値は0.0に近い方が良いモデルということになります。
平均絶対誤差(MAE) Mean Absolute Error
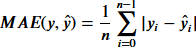
観測値と予測値の差の絶対値の平均。
全てのサンプルの誤差を合計してサンプル数で割ることで、サンプル1つあたりの誤差を計算します。
from sklearn.metrics import mean_absolute_error
ret = mean_absolute_error(y_true, y_pred, [sample_weight], [multioutput])
変数 |
型 |
内容 |
|---|---|---|
y_true |
array-like |
正しい値(観測値) |
y_pred |
array-like |
予測値 |
sample_weight |
array-like |
省略可。既定値はNone。ウェイト。 |
multioutput |
array-like, str |
省略可。既定値は'uniform_average'。 複数出力に対する指定。 |
ret |
float, ndaray |
差の絶対値の平均。 |
y_trueとy_predの型は、リストやpandas.Seriesなどです。
戻り値は0.0に近い方が良いモデルということになります。
y_trueとy_predが2次元のとき、multioutputをraw_valueにすると各次元毎に平均絶対誤差を計算してndarrayの形で返します。multioutputをuniform_averageにすると、各平均絶対誤差の平均を返します。
平均二乗誤差(MSE) Mean Squared Error
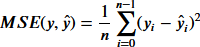
観測値と予測値の差の2乗の平均。
各サンプル毎の誤差を2乗して合計し、サンプル1つあたりどれくらいになるのか計算します。誤差を2乗するので、誤差が大きいサンプルが存在するとMAEよりも大きな値になります。
from sklearn.metrics import mean_squared_error
ret = mean_squared_error(y_true, y_pred, [sample_weight], [multioutput], [squared])
変数 |
型 |
内容 |
|---|---|---|
y_true |
array-like |
正しい値(観測値) |
y_pred |
array-like |
予測値 |
sample_weight |
array-like |
省略可。既定値はNone。ウェイト。 |
multioutput |
array-like, str |
省略可。既定値は'uniform_average'。 複数出力に対する指定。 |
squared |
boot |
省略可。既定値はTrue。計算結果を平方根で出力しないか。 |
ret |
float, ndaray |
差の絶対値の平均。 |
y_trueとy_predの型は、リストやpandas.Seriesなどです。
戻り値は0.0に近い方が良いモデルということになります。
y_trueとy_predが2次元のとき、multioutputをraw_valueにすると各次元毎に平均絶対誤差を計算してndarrayの形で返します。multioutputをuniform_averageにすると、各平均絶対誤差の平均を返します。
squaredをTrueにすると平均二乗誤差を、Falseにすると次項の二乗平均平方根誤差を返します。
二乗平均平方根誤差(RMSE) Root Mean Squared Error
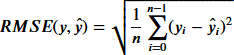
観測値と予測値の差の2乗の平均(MSE)の平方根。
誤差を2乗していることから、MAEよりも外れ値の影響を受けやすくなります。平方根をとることで、MSEよりも敏感ではなくなります。
Scikit-learnで計算する場合には、前項で述べたmean_squared_error関数を使用します。関数のsquared引数にFalseをセットすることに注意してください。
mean_squared_errorにsquared引数を指定できない環境では、numpy.squre関数で平方根を求めます。
各誤差を計算してみる
実際に誤差を計算してみます。同じデータに対して、評価関数によって値が異なります。
誤差を計算するデータ
このようなDataFrameを作りました。
import pandas as pd
data = pd.DataFrame([0,1,2,3,4,5], columns=['x'])
data['y'] = data['x']
data['y1'] = data['x']+2
data['y2'] = [2,3,0,1,2,7]
data['y3'] = [2,3,8,5,6,7]
print(data.head(10))
x y y1 y2 y3
0 0 0 2 2 2
1 1 1 3 3 3
2 2 2 4 0 8
3 3 3 5 1 5
4 4 4 6 2 6
5 5 5 7 7 7
説明変数xに対して目的変数がy=xになる事象についてのモデルの予測値が、y1、y2、y3の3種類あるとしたものです。各予測値y1、y2、y3と真値yの誤差を計算していきます。
予測値が一定にずれている場合
yとy1をグラフに表すとこのようになります。
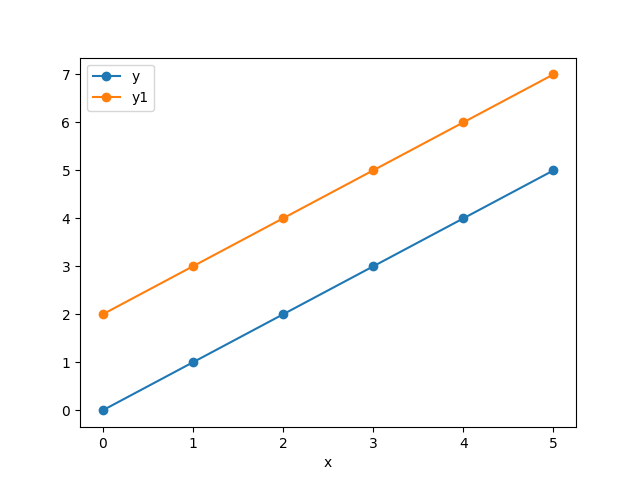
このような観測値と予測値に対して、各評価関数で誤差を計算すると下記のようになります。
from matplotlib import pyplot as plt
import pandas as pd
from sklearn.metrics import max_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
data = pd.DataFrame([0,1,2,3,4,5], columns=['x'])
data['y'] = data['x']
data['y1'] = data['x']+2
data['y2'] = [2,3,0,1,2,7]
data['y3'] = [2,3,8,5,6,7]
data.plot.line(x='x', y=['y','y1'], marker='o')
plt.show()
print('MaxError', max_error(data['y'], data['y1']))
print('MAE', mean_absolute_error(data['y'], data['y1']))
print('MSE', mean_squared_error(data['y'], data['y1']))
print('RMSE', mean_squared_error(data['y'], data['y1'], squared=False))
MaxError 2
MAE 2.0
MSE 4.0
RMSE 2.0
正負が異なるデータがある場合
一般的には真値(観測値)に対して予測値は上回ったり下回ったりするわけですので、そういう場合はどうなるでしょうか。
yとy2をグラフに表すとこのようになります。
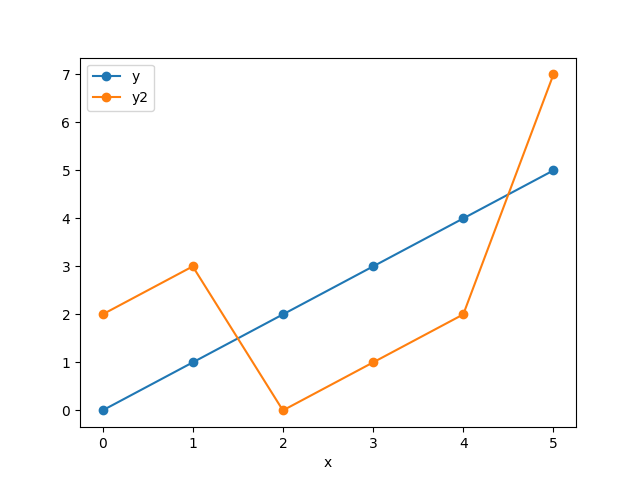
このような観測値と予測値に対して、各評価関数で誤差を計算すると下記のようになります。
from matplotlib import pyplot as plt
import pandas as pd
from sklearn.metrics import max_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
data = pd.DataFrame([0,1,2,3,4,5], columns=['x'])
data['y'] = data['x']
data['y1'] = data['x']+2
data['y2'] = [2,3,0,1,2,7]
data['y3'] = [2,3,8,5,6,7]
data.plot.line(x='x', y=['y','y2'], marker='o')
plt.show()
print('MaxError', max_error(data['y'], data['y2']))
print('MAE', mean_absolute_error(data['y'], data['y2']))
print('MSE', mean_squared_error(data['y'], data['y2']))
print('RMSE', mean_squared_error(data['y'], data['y2'], squared=False))
MaxError 2
MAE 2.0
MSE 4.0
RMSE 2.0
観測値と予測値の距離をもとに計算しているのであって、向き(プラスかマイナスか)は関係ないことがわかりますね。
外れ値がある場合
外れ値がある場合を試してみます。
yとy3をグラフに表すとこのようになります。
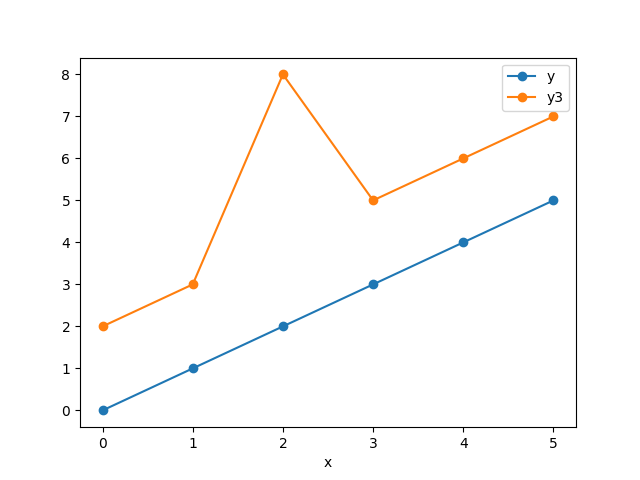
このような観測値と予測値に対して、各評価関数で誤差を計算すると下記のようになります。
from matplotlib import pyplot as plt
import pandas as pd
from sklearn.metrics import max_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
data = pd.DataFrame([0,1,2,3,4,5], columns=['x'])
data['y'] = data['x']
data['y1'] = data['x']+2
data['y2'] = [2,3,0,1,2,7]
data['y3'] = [2,3,8,5,6,7]
data.plot.line(x='x', y=['y','y3'], marker='o')
plt.show()
print('MaxError', max_error(data['y'], data['y3']))
print('MAE', mean_absolute_error(data['y'], data['y3']))
print('MSE', mean_squared_error(data['y'], data['y3']))
print('RMSE', mean_squared_error(data['y'], data['y3'], squared=False))
MaxError 6
MAE 2.6666666666666665
MSE 9.333333333333334
RMSE 3.0550504633038935
MSE(平均二乗誤差)が外れ値に対する反応が大きいことがわかります。これでは敏感すぎるということであれば、RMSE(二乗平均平方根誤差)がMSEほど大きな値にはならないがMAE(平均絶対誤差)よりは敏感に反応することがわかります。
公開日
広告
Pythonでデータ分析カテゴリの投稿
- DataFrameの欠損値を特定の値で置き換える
- Pythonでpandas入門1(データの入力とデータへのアクセス)
- Pythonでpandas入門2(データの追加と削除および並び替え)
- Pythonでpandas入門3(データの統計量の計算)
- Pythonでpandas入門4(データの連結と結合)
- Pythonでpandas入門5(欠損値(NaN)の扱い)
- Pythonでデータを学習用と検証用に分割する
- Pythonでデータ分析入門1(初めての回帰分析)
- Pythonでデータ分析入門2(初めてのロジスティック回帰(2クラス分類))
- Pythonでデータ分析入門3(初めての決定木(多クラス分類))
- Pythonで回帰モデルの評価関数
- Pythonで箱ひげ図を描く
- Python(pandas)でExcelファイルを読み込んでDataFrameにする
- pandasでカテゴリ変数を数値データに変換する
- pandasでクロス集計する
- pandasで同じデータ(要素)がいくつあるか調べる
- pandasで相関係数を計算する
- pandasとseabornでデータの可視化(散布図行列)
- pandasの学習用のデータセットを入手する
- scikit-learnのサンプルデータセットを入手する