Chainerのチュートリアルを試してみた(畳み込みを深くする編)
Chainerのチュートリアルを試してみました。層をブロックにして、深いネットワークを作ってみます。
目次
チュートリアルの内容
Chainerのチュートリアルは本家でも公開されてますが、今回試してみたのは こちらのサイトのもの です。リンク先のサイトではJupyter notebookを使う前提で書かれているのですが、本投稿ではローカル環境でのPythonで実行します。
実行した環境は、Windows10 64bit、Python 3.7、Chainer 6.1、CUDA 10.1です。
CIFAR10の画像の分類をします。
データセットの準備
Chainerの便利機能でダウンロードして分割したCIFAR10のデータセットを使用します。ダウンロードの方法は 以前の投稿 の「データセットのダウンロード」の箇所を参照してください。
深いネットワークを作る
畳み込み層と前後する一連の層や、全結合層と前後する一連の層を塊(ブロック)にして、そのブロックをつなげることで深い(長い)ネットワークを作ります。今回作るネットワーク全体はこんな感じです。
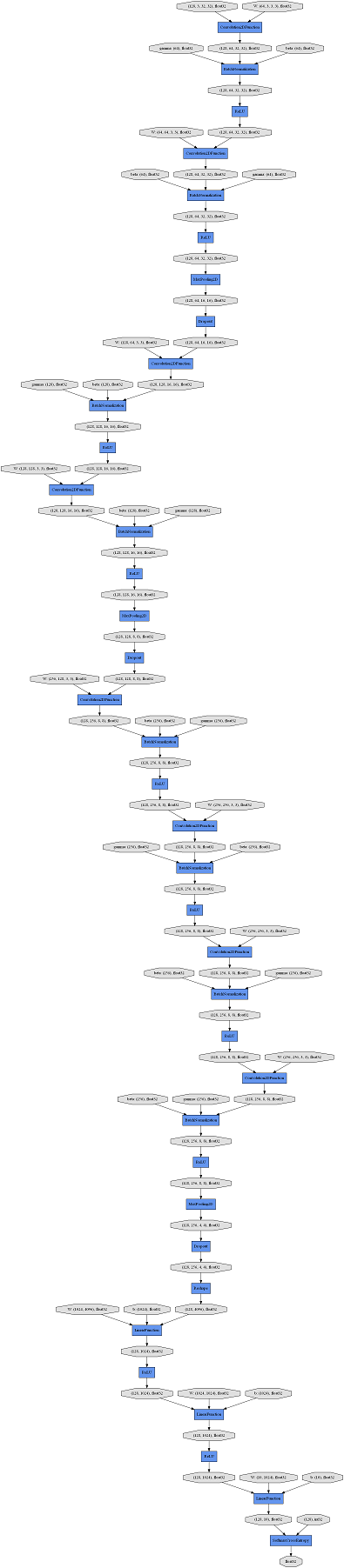
ConvBlockというクラスは、畳み込み層のブロックを定義するクラスです。入力に対して、畳み込み、バッチ正規化、ReLU(、マックスプーリング、ドロップアウト)をひとまとめにしています。
LinearBlockというクラスは、全結合層のブロックを定義するクラスです。入力に対して、全結合、ReLU(、ドロップアウト)をひとまとめにしています。
このブロックの中にifで分岐を書けるのですね。
これらのブロックをDeepCNNというChainListを継承したクラスに列挙することで、深いネットワークを作ります。
import pickle
import numpy
import random
import chainer
import chainer.cuda
import cupy
import chainer.links as L
import chainer.functions as F
from chainer import iterators
from chainer import optimizers
from chainer import training
from chainer.training import extensions
from chainer import serializers
# 畳み込み層部分の定義をするクラス
class ConvBlock(chainer.Chain):
def __init__(self, n_ch, pool_drop=False):
w = chainer.initializers.HeNormal()
super(ConvBlock, self).__init__()
with self.init_scope():
self.conv = L.Convolution2D(None, n_ch, 3, 1, 1, nobias=True, initialW=w) # 畳み込み層
self.bn = L.BatchNormalization(n_ch) # バッチノーマリゼーション層
self.pool_drop = pool_drop
def __call__(self, x):
h = F.relu(self.bn(self.conv(x))) # 入力を畳み込んで、バッチ正規化して、ReLUを通す
if self.pool_drop: # pool_dorpがTrueのときは、マックスプーリングして、ドロップアウトする
h = F.max_pooling_2d(h, 2, 2)
h = F.dropout(h, ratio=0.25)
return h
# 全結合層部分の定義をするクラス
class LinearBlock(chainer.Chain):
def __init__(self, drop=False):
w = chainer.initializers.HeNormal()
super(LinearBlock, self).__init__()
with self.init_scope():
self.fc = L.Linear(None, 1024, initialW=w) # 全結合層
self.drop = drop
def __call__(self, x):
h = F.relu(self.fc(x)) # 入力を全結合して、ReLuを通す
if self.drop: # dropがTrueのときは、ドロップアウトする
h = F.dropout(h)
return h
# ネットワーク全体の定義をするクラス
class DeepCNN(chainer.ChainList):
def __init__(self, n_output):
super(DeepCNN, self).__init__(
ConvBlock(64),
ConvBlock(64, True),
ConvBlock(128),
ConvBlock(128, True),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256, True),
LinearBlock(),
LinearBlock(),
L.Linear(None, n_output)
)
def __call__(self, x):
for f in self:
x = f(x)
return x
# 学習を実行する関数
def train(network_object, batchsize=128, gpu_id=0, max_epoch=20, train_dataset=None, valid_dataset=None, test_dataset=None, postfix='', base_lr=0.01, lr_decay=None):
# 1. データセットの読み込み
with open('test.pickle', mode='rb') as fi1:
test = pickle.load(fi1)
with open('train.pickle', mode='rb') as fi2:
train = pickle.load(fi2)
with open('valid.pickle', mode='rb') as fi3:
valid = pickle.load(fi3)
# 2. イテレーターの作成(データセットをバッチで取り出せるようにする)
train_iter = iterators.SerialIterator(train, batchsize)
valid_iter = iterators.SerialIterator(valid, batchsize, False, False)
# 3. ネットワークのインスタンスを作る
net = L.Classifier(network_object)
# 4. オプティマイザーの作成(学習量の計算の設定)
optimizer = optimizers.MomentumSGD(lr=base_lr).setup(net)
optimizer.add_hook(chainer.optimizer.WeightDecay(0.0005))
# 5. アップデーターの作成(ネットワークのパラメーターのアップデート)
updater = training.StandardUpdater(train_iter, optimizer, device=gpu_id)
# 6. トレーナーの作成(学習サイクルの実行)
trainer = training.Trainer(updater, (max_epoch, 'epoch'), out='{}_cifar10_{}result'.format(network_object.__class__.__name__, postfix))
# 7. トレーナーのオプションの設定
trainer.extend(extensions.LogReport())
trainer.extend(extensions.observe_lr())
trainer.extend(extensions.Evaluator(valid_iter, net, device=gpu_id), name='val')
trainer.extend(extensions.PrintReport(['epoch', 'main/loss', 'main/accuracy', 'val/main/loss', 'val/main/accuracy', 'elapsed_time', 'lr']))
trainer.extend(extensions.PlotReport(['main/loss', 'val/main/loss'], x_key='epoch', file_name='loss.png'))
trainer.extend(extensions.PlotReport(['main/accuracy', 'val/main/accuracy'], x_key='epoch', file_name='accuracy.png'))
trainer.extend(extensions.dump_graph('main/loss'))
if lr_decay is not None:
trainer.extend(extensions.ExponentialShift('lr', 0.1), trigger=lr_decay)
trainer.run()
del trainer
# 8. 評価
test_iter = iterators.SerialIterator (test, batchsize, False, False)
test_evaluator = extensions.Evaluator(test_iter, net, device=gpu_id)
results = test_evaluator()
print('Test accuracy:', results['main/accuracy'])
return net
# 乱数を初期化する関数
def reset_seed(seed=0):
random.seed(seed)
numpy.random.seed(seed)
if chainer.cuda.available:
chainer.cuda.cupy.random.seed(seed)
# cuDNNのautotuneを有効にする
chainer.cuda.set_max_workspace_size(512 * 1024 * 1024)
chainer.config.autotune = True
# 乱数の初期化
reset_seed(0)
# 学習の実行
net = train(DeepCNN(10), max_epoch=100, base_lr=0.1, lr_decay=(30, 'epoch'))
# 学習結果の保存
serializers.save_npz('my_cifar10.model', net)
今回はGPUで計算しますので、autotuneを有効にしてみました。
Visual Studio Codeのpylintがchainer.cudaのメンバーが無いという警告を出してきたのでちょっと焦りましたが、問題なくGPUで計算してくれたようです。
epoch main/loss main/accuracy val/main/loss val/main/accuracy elapsed_time lr
1 2.6437 0.144531 2.2232 0.16582 20.6501 0.1
2 2.12134 0.207919 2.00311 0.267578 39.8627 0.1
3 1.88175 0.28835 1.96174 0.292969 58.8182 0.1
4 1.73099 0.345503 1.77057 0.312891 77.8201 0.1
5 1.57302 0.417713 1.6491 0.391016 96.6805 0.1
6 1.37428 0.496316 1.44605 0.480273 115.618 0.1
7 1.20373 0.565104 1.195 0.567578 134.556 0.1
8 1.09236 0.609397 1.2061 0.573438 153.542 0.1
9 0.983244 0.65261 1.04837 0.649805 172.479 0.1
10 0.910236 0.679532 0.890074 0.689648 191.431 0.1
11 0.839646 0.710005 1.12711 0.637891 210.407 0.1
12 0.777537 0.73275 1.24749 0.60293 229.283 0.1
13 0.750183 0.742188 0.823973 0.72168 248.311 0.1
14 0.702904 0.76035 0.71562 0.75332 267.239 0.1
15 0.674656 0.769664 0.906134 0.70332 286.208 0.1
16 0.659935 0.779336 0.753152 0.737109 305.08 0.1
17 0.617898 0.791926 0.633969 0.785547 324.063 0.1
18 0.603082 0.798074 0.989168 0.675977 343.001 0.1
19 0.587477 0.803641 0.802272 0.747656 361.917 0.1
20 0.569411 0.809104 0.843102 0.726953 380.843 0.1
21 0.557242 0.811944 0.705192 0.762891 399.715 0.1
22 0.538812 0.822088 1.57609 0.574023 418.659 0.1
23 0.527007 0.821937 0.711417 0.783594 437.541 0.1
24 0.527024 0.82342 1.01725 0.662109 456.515 0.1
25 0.504342 0.829967 0.98378 0.703125 475.428 0.1
26 0.499243 0.833178 0.943754 0.702539 494.347 0.1
27 0.498686 0.833341 2.72165 0.434961 513.275 0.1
28 0.477141 0.840589 0.789254 0.74375 532.147 0.1
29 0.471671 0.841819 0.669663 0.788477 551.122 0.1
30 0.476996 0.84148 0.586559 0.80293 570.04 0.1
31 0.300428 0.897905 0.39851 0.877148 588.969 0.01
32 0.221266 0.92488 0.36525 0.881641 607.863 0.01
33 0.191751 0.933993 0.357381 0.89043 626.788 0.01
34 0.170519 0.941628 0.347432 0.892969 645.745 0.01
35 0.153229 0.946136 0.357087 0.886328 664.709 0.01
36 0.140532 0.951127 0.354779 0.889648 683.689 0.01
37 0.13109 0.95426 0.361992 0.891016 702.585 0.01
38 0.118159 0.958629 0.392906 0.887695 721.536 0.01
39 0.109702 0.962362 0.387895 0.889258 740.475 0.01
40 0.102641 0.964134 0.405599 0.888281 759.706 0.01
41 0.0972486 0.966397 0.394764 0.892773 778.749 0.01
42 0.0915414 0.967993 0.402179 0.892773 797.765 0.01
43 0.0863423 0.970104 0.412282 0.888477 816.733 0.01
44 0.0878853 0.969306 0.432859 0.882422 835.611 0.01
45 0.078483 0.972168 0.432829 0.883984 854.549 0.01
46 0.0750526 0.97447 0.412971 0.892187 873.462 0.01
47 0.0684961 0.976318 0.420595 0.890039 892.409 0.01
48 0.0686924 0.976451 0.478586 0.880273 911.282 0.01
49 0.070054 0.975852 0.444838 0.883008 930.2 0.01
50 0.0713485 0.975053 0.433133 0.884961 949.11 0.01
51 0.0656244 0.977364 0.465228 0.885156 967.978 0.01
52 0.0604113 0.979115 0.467371 0.878516 986.931 0.01
53 0.0677948 0.976496 0.467753 0.880078 1005.82 0.01
54 0.0590325 0.979359 0.491907 0.88125 1024.74 0.01
55 0.0612465 0.978966 0.451046 0.886914 1043.63 0.01
56 0.0653968 0.977472 0.49247 0.879297 1062.62 0.01
57 0.060906 0.979137 0.481422 0.882422 1081.63 0.01
58 0.06187 0.979167 0.467294 0.886523 1100.55 0.01
59 0.0618526 0.978826 0.468995 0.88457 1119.48 0.01
60 0.0565759 0.980257 0.567624 0.86543 1138.38 0.01
61 0.0374251 0.98746 0.415678 0.892773 1157.38 0.001
62 0.0229866 0.993122 0.419805 0.891602 1176.31 0.001
63 0.0192019 0.994074 0.419598 0.894336 1195.31 0.001
64 0.0174565 0.994925 0.422318 0.897656 1214.2 0.001
65 0.0162033 0.994851 0.427115 0.897656 1233.15 0.001
66 0.0150596 0.995472 0.429711 0.896484 1252.13 0.001
67 0.012677 0.996439 0.432503 0.895703 1271.12 0.001
68 0.0118089 0.99656 0.437222 0.898828 1290.15 0.001
69 0.0129675 0.996216 0.444267 0.896094 1309.03 0.001
70 0.0108742 0.996893 0.444565 0.900195 1327.97 0.001
71 0.01087 0.996995 0.447843 0.89707 1346.84 0.001
72 0.00934628 0.997314 0.450479 0.898242 1365.84 0.001
73 0.00934687 0.997181 0.459053 0.898633 1384.83 0.001
74 0.00939448 0.997106 0.460052 0.899219 1403.78 0.001
75 0.00902866 0.997514 0.455976 0.899023 1422.77 0.001
76 0.00872597 0.997507 0.465737 0.898633 1442 0.001
77 0.0093198 0.997026 0.46898 0.898633 1461.14 0.001
78 0.00859233 0.997396 0.460254 0.898047 1480.13 0.001
79 0.00779859 0.997803 0.463143 0.899805 1499.1 0.001
80 0.00736309 0.997975 0.459977 0.899805 1518.02 0.001
81 0.0081748 0.99747 0.464284 0.897461 1537.02 0.001
82 0.00776547 0.997714 0.462811 0.898438 1556.03 0.001
83 0.00709248 0.998108 0.466836 0.9 1575.1 0.001
84 0.00721658 0.99818 0.467964 0.898828 1594.38 0.001
85 0.00739202 0.997997 0.467479 0.899609 1613.31 0.001
86 0.00681072 0.998202 0.458913 0.900195 1632.22 0.001
87 0.00629826 0.998353 0.46128 0.899609 1651.1 0.001
88 0.00676739 0.997958 0.467949 0.9 1670.01 0.001
89 0.00704037 0.998291 0.472412 0.902148 1688.89 0.001
90 0.00633939 0.998197 0.466698 0.899219 1707.76 0.001
91 0.00567754 0.998691 0.462024 0.9 1726.76 0.0001
92 0.00576062 0.998642 0.461816 0.898242 1745.61 0.0001
93 0.00595025 0.998668 0.462708 0.899219 1764.62 0.0001
94 0.00589382 0.998353 0.463547 0.9 1783.62 0.0001
95 0.00611592 0.998335 0.459985 0.900781 1802.67 0.0001
96 0.00645041 0.998064 0.461833 0.9 1821.66 0.0001
97 0.00565064 0.998491 0.460635 0.900586 1840.71 0.0001
98 0.00585507 0.998491 0.459271 0.899414 1859.62 0.0001
99 0.00535949 0.998665 0.468896 0.9 1878.5 0.0001
100 0.00535571 0.998668 0.466266 0.901172 1897.59 0.0001
Test accuracy: 0.89685524
精度がおよそ90%になりました。
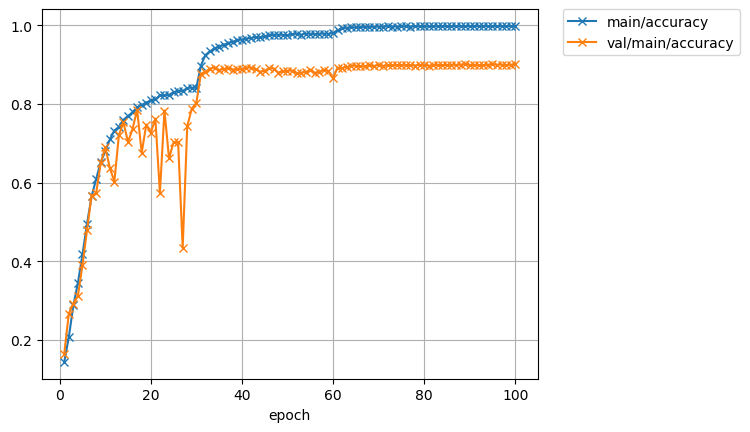
30エポックのあたり(学習率Ir)を小さくしたところでガンッと精度が上がってます。
推論してみた
では学習したモデルを使って、テストデータの推定をしてみます。
今回は、100枚のテスト画像に対して、教師データと推定値が異なるものだけを表示するようにしてみました。
import pickle
import matplotlib.pyplot as plt
import chainer
import chainer.links as L
import chainer.functions as F
from chainer import serializers
# 畳み込み層部分の定義をするクラス
class ConvBlock(chainer.Chain):
def __init__(self, n_ch, pool_drop=False):
w = chainer.initializers.HeNormal()
super(ConvBlock, self).__init__()
with self.init_scope():
self.conv = L.Convolution2D(None, n_ch, 3, 1, 1, nobias=True, initialW=w) # 畳み込み層
self.bn = L.BatchNormalization(n_ch) # バッチノーマリゼーション層
self.pool_drop = pool_drop
def __call__(self, x):
h = F.relu(self.bn(self.conv(x))) # 入力を畳み込んで、バッチ正規化して、ReLUを通す
if self.pool_drop: # pool_dorpがTrueのときは、マックスプーリングして、ドロップアウトする
h = F.max_pooling_2d(h, 2, 2)
h = F.dropout(h, ratio=0.25)
return h
# 全結合層部分の定義をするクラス
class LinearBlock(chainer.Chain):
def __init__(self, drop=False):
w = chainer.initializers.HeNormal()
super(LinearBlock, self).__init__()
with self.init_scope():
self.fc = L.Linear(None, 1024, initialW=w) # 全結合層
self.drop = drop
def __call__(self, x):
h = F.relu(self.fc(x)) # 入力を全結合して、ReLuを通す
if self.drop: # dropがTrueのときは、ドロップアウトする
h = F.dropout(h)
return h
# ネットワーク全体の定義をするクラス
class DeepCNN(chainer.ChainList):
def __init__(self, n_output):
super(DeepCNN, self).__init__(
ConvBlock(64),
ConvBlock(64, True),
ConvBlock(128),
ConvBlock(128, True),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256),
ConvBlock(256, True),
LinearBlock(),
LinearBlock(),
L.Linear(None, n_output)
)
def __call__(self, x):
for f in self:
x = f(x)
return x
# 推論を実行する関数
def predict(net, image_id):
x, t = test[image_id]
with chainer.using_config('train', False), chainer.using_config('enable_backprop', False):
y = net.predictor(x[None, ...]).data.argmax(axis=1)[0]
if t != y:
plt.imshow(x.transpose(1, 2, 0))
plt.text(1,1, cls_names[t], color='red')
plt.text(1,2, cls_names[y], color='red')
plt.show()
# テストデータのラベル
cls_names = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
# テストデータの読み込み
with open('test.pickle', mode='rb') as fi1:
test = pickle.load(fi1)
# ネットワークのインスタンスの作成
infer_net = L.Classifier(DeepCNN(10))
# ネットワークの学習済みパラメーターの読み込み
serializers.load_npz('my_cifar10.model', infer_net)
# 推論の実行
for i in range(10, 110):
predict(infer_net, i)
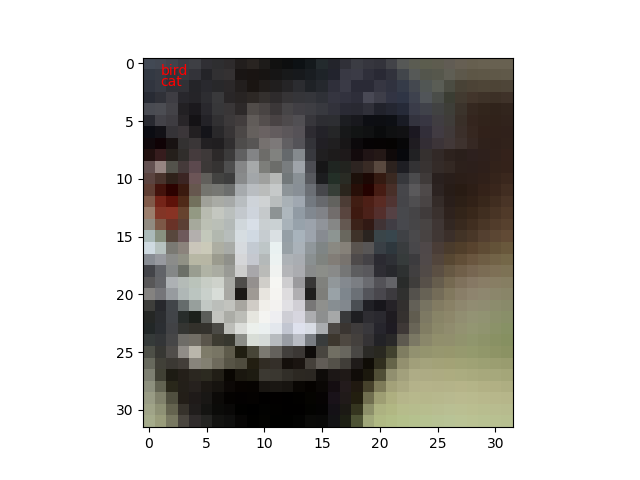
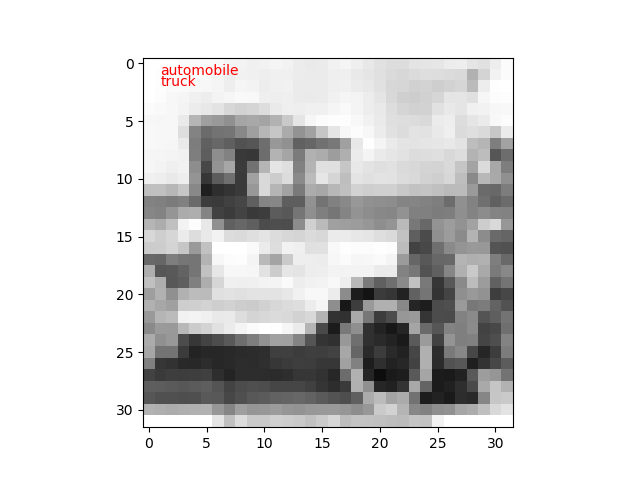
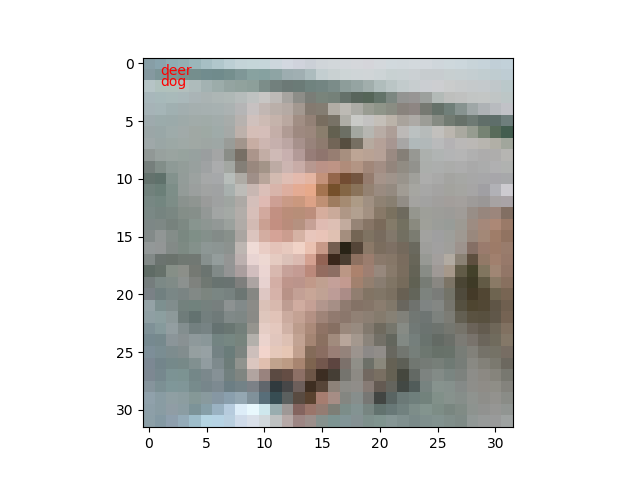
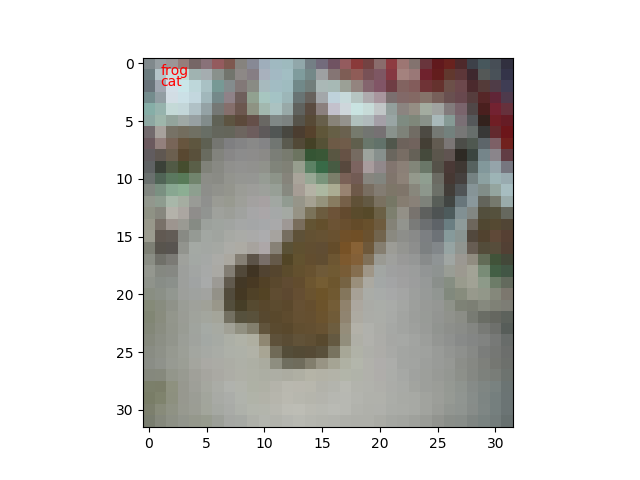
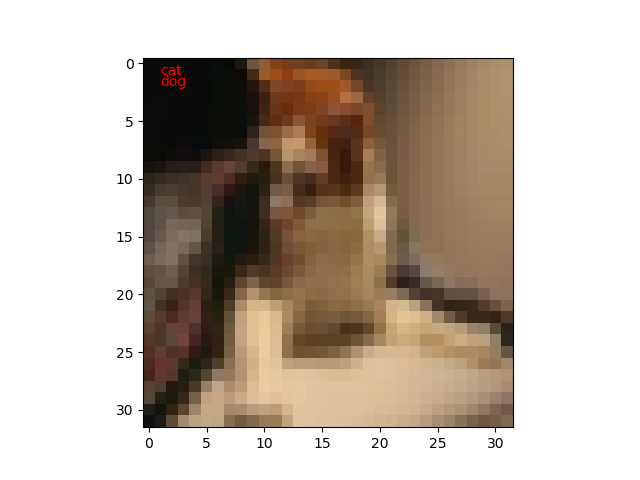
私も間違えそうな画像があります。
公開日
広告
Chainerカテゴリの投稿
- ChainerCVで使える画像のデータ拡張
- ChainerCVで画像を出力する方法
- ChainerCVのResNetを使う
- ChainerCVのSSDに学習させてみた
- ChainerCVのデモンストレーションプログラムを読んでみた
- ChainerCVのデモンストレーションプログラムを読んでみた(推論編)
- Chainerが出力するネットワーク構造図をGraphvizで見る
- Chainerで数字を分類してみた
- ChainerのSSDのデモで物体検出をしてみる
- Chainerのチュートリアルを試してみた
- Chainerのチュートリアルを試してみた(ChainerCVでデータ拡張編)
- Chainerのチュートリアルを試してみた(データ拡張編)
- Chainerのチュートリアルを試してみた(トレーナー編)
- Chainerのチュートリアルを試してみた(畳み込みを深くする編)
- Chainerのチュートリアルを試してみた(畳み込み編)
- Chainerのデータセットの作り方(ラベル付き画像編)
- VoTTのPascal VOC出力をChainerCVのデータセットとして読み込んでみた