Chainerチュートリアルでscikit-learnに入門した(重回帰分析)
PFNのChainerチュートリアルのscikit-learnの入門編をやってみました。
目次
- チュートリアルの内容
- データのダウンロード
- データの中身を確認する
- データセットの分割
- モデル、目的関数、最適化手法をを決めて、訓練する
- 推論
- テスト用データセットでモデルを評価する
- データの標準化
- データの標準化(べき変換)
チュートリアルの内容
機械学習の一つとして、ボストンの家賃をscikit-learnを使って重回帰分析をして予測します。
PFNのチュートリアル ではGoogle colabを使用していますが、本投稿ではローカルで実行します。
scikit-learnはpipでインストールできます。
> pip install scikit-learn
データのダウンロード
学習に使用するボストンの地域毎のデータセットをダウンロードします。ダウンロードは、scikit-learnに組み込まれているダウンロード機能を使用します。
データサイズは数十キロバイトくらいの大きさですが、試行錯誤するたびにダウンロードするのは申し訳ないので、ダウンロードしたデータをpickleで保存しておきます。pickleの使い方は 以前の投稿 を参考にしてください。
from sklearn.datasets import load_boston
import pickle
dataset = load_boston()
with open('skl_boston_data.pickle', mode='wb') as f:
pickle.dump(dataset, f)
インターネットにつないだ状態で上記のコードを実行すると、ダウンロードしたデータがskl_boston_data.pickleというファイルに保存されるはずです。以降のプログラムでは、このpickleファイルを読み込むようにします。
データの中身を確認する
データセットには、dataとtargetとDESCRというプロパティがあります。dataが学習に使うデータ、targetが目標になるデータ、DESCRがデータの説明です。データに何が含まれているのかDESCRに記載されています。ちょっと見てみましょう。
import pickle
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
description = dataset.DESCR
print(description)
出力(抜粋)
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
ボストンを506の地域に分割して、各地域のプロパティー(CRIM等)が並べてあるということでしょうか。
チュートリアルに沿って、データの形状を見てみましょう。ついでに、データセットからデータを1つ取り出してどういうデータが入っているか見てみます。
import pickle
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
print('data shape : ', x.shape)
print('target shape : ', t.shape)
print(x[0])
出力
data shape : (506, 13)
target shape : (506,)
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00]
これは、犯罪発生率が0.632%で、宅地の割合が18%で、ということですね。
データセットの分割
学習用のデータを、訓練用データとテスト用データに分割します。訓練用データで学習して、テスト用データでその成果を確認するわけですね。
データの分割にはscikit-learnのメソッド(train_test_split)を使用します。チュートリアルに従って、7:3で分けてみます。
import pickle
from sklearn.model_selection import train_test_split
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
print('x_train : ', x_train.shape)
print('x_test : ', x_test.shape)
print('t_train : ', t_train.shape)
print('t_test : ', t_test.shape)
出力
x_train : (354, 13)
x_test : (152, 13)
t_train : (354,)
t_test : (152,)
506個のデータの70%ですから、354個ですね。
モデル、目的関数、最適化手法をを決めて、訓練する
本家のチュートリアルでは分けてますが、ここではパラメータ-とバイアスおよび精度の出力までまとめて行います。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
reg_model = LinearRegression()
reg_model.fit(x_train, t_train)
print('parameter : \n', reg_model.coef_)
print('bias : ', reg_model.intercept_)
print('score : ', reg_model.score(x_train, t_train))
出力
parameter :
[-1.21310401e-01 4.44664254e-02 1.13416945e-02 2.51124642e+00
-1.62312529e+01 3.85906801e+00 -9.98516565e-03 -1.50026956e+00
2.42143466e-01 -1.10716124e-02 -1.01775264e+00 6.81446545e-03
-4.86738066e-01]
bias : 37.937107741831994
score : 0.7645451026942549
scikit-learnの重回帰分析用のクラスはLinearRegressionクラスです。これをオブジェクト(reg_model)にして、そのオブジェクトのfitメソッドで訓練を行います。
訓練したオブジェクトのcoefプロパティに重回帰分析のパラメーターが、interceptプロパティにバイアスが格納されます。
オブジェクトのscoreメソッドにデータを渡すと、精度が計算されます。訓練データでの精度は0.76でした。
推論
テスト用のデータを使って推論してみます。推論するための学習ですからね。
推論には、LinearRegressionオブジェクトのpredictメソッドを使用します。下記のプログラムでは、推論の結果と目標値を表示します。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
reg_model = LinearRegression()
reg_model.fit(x_train, t_train)
print('predict : ', reg_model.predict(x_test[:1]))
print('target : ', t_test[0])
出力
predict : [24.9357079]
target : 22.6
チュートリアルと同じようにずれてますね。
テスト用データセットでモデルを評価する
モデルがどれくらいの精度で推論するのか、テスト用のデータセットを使って精度を計算します。といっても、scoreメソッドにテスト用のデータを与えるだけですが。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
reg_model = LinearRegression()
reg_model.fit(x_train, t_train)
print('score : ', reg_model.score(x_test, t_test))
出力
score : 0.6733825506400202
訓練用データでの精度が0.76でしたので、少し訓練用データに最適化されているのかもしれません。
データの標準化
チュートリアルに習って、データの標準化をします。
チュートリアルでは、サラっとStandardScalerクラスを使って平均と分散を計算して標準化すると書かれています。
標準化というのは、データの平均を0に、分散(標準偏差)を1にすることで、項目間のデータの大小を比較できるようにするものです。
元のデータをx、平均をxa、標準偏差をsとしたときに、標準化したデータは(x - xa)/sとなります。
ちなみに、元のデータのうちの1つを標準化するとこうなります。
# 元データ
[ 1.62864 0. 21.89 0. 0.624 5.019 100.
1.4394 4. 437. 21.2 396.9 34.41 ]
# 標準化後
[-0.20735619 -0.49997924 1.54801583 -0.26360274 0.58821309 -1.83936729 1.10740225
-1.1251102 -0.61816013 0.20673466 1.2272573 0.42454294 3.10807269]
元のデータは項目によってレンジがバラバラだったのですが、標準化すると同じレンジで比較できるようになります。
では、標準化したデータで訓練して、精度を比較してみます。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
scaler = StandardScaler()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_test_scaled = scaler.transform(x_test)
reg_model = LinearRegression()
reg_model.fit(x_train_scaled, t_train)
print('score train : ', reg_model.score(x_train_scaled, t_train))
print('score test : ', reg_model.score(x_test_scaled, t_test))
出力
score train : 0.7645451026942549
score test : 0.6733825506400196
標準化しても効果はありませんでした。
データの標準化(べき変換)
チュートリアルではサラっと「べき変換する」と書かれています。
べき変換というのは、データを正規分布に近くなるように正規化する変換です。scikit-learnではPowerTransformerクラスがべき変換を行うクラスです。べき変換の変換手法として2種類(Box-CoxとYeo-Johnson)あるのですが、scikit-learnのPowerTransformerクラスの既定の方法はYeo-Johnson法です。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PowerTransformer
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
scaler = PowerTransformer()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_test_scaled = scaler.transform(x_test)
reg_model = LinearRegression()
reg_model.fit(x_train_scaled, t_train)
print('score train : ', reg_model.score(x_train_scaled, t_train))
print('score test : ', reg_model.score(x_test_scaled, t_test))
出力
score train : 0.7859862562650238
score test : 0.7002856552456189
データ標準化前のテスト用データでの精度が0.67でしたから、少し精度が向上しました。
では推論してみましょう。テスト用データの1番目のデータで推論してみます。
import pickle
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PowerTransformer
with open('skl_boston_data.pickle', mode='rb') as f:
dataset = pickle.load(f)
x = dataset.data
t = dataset.target
x_train, x_test, t_train, t_test = train_test_split(x, t, test_size=0.3, random_state=0)
scaler = PowerTransformer()
scaler.fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_test_scaled = scaler.transform(x_test)
reg_model = LinearRegression()
reg_model.fit(x_train_scaled, t_train)
print('predict : ', reg_model.predict(x_test_scaled[:1]))
print('target : ', t_test[0])
出力
predict : [27.25834943]
target : 22.6
う~ん、データ全体の精度は上がっても、個々の精度が上がるとは限らないのか。
テスト用の各データの目標値と推論値をプロットしてみます。
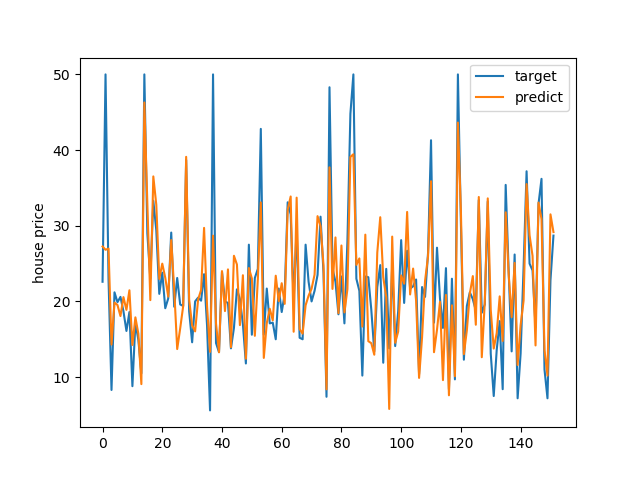
近似しているといえば近似してるかな。
公開日
広告